ENERGY_PERFORMANCE_ASSESSMENT_FOR_EQUIPMENT_AND UTILITY SYSTEMS
(Chapter 4:Energy Performance Assessment of Heat Exchangers)
Introduction
Heat exchangers are equipment that transfers heat from one medium to another. Shell and tube heat exchangers are used extensively through out the process and power industry and as such a basic understanding of their design, construction and performance is important to the practicing engineer. The proper design, operation and maintenance of heat exchangers will make the process energy efficient and minimize energy losses.
Purpose of the Performance Test
Heat exchanger performance can deteriorate with time, off design operations and other interferences such as fouling, scaling, corrosion etc. It is necessary to assess periodically the heat exchanger performance in order to maintain them at a high efficiency level. This section comprises certain proven techniques of monitoring the performance of heat exchangers, coolers and condensers from observed operating data of the equipment. The objective of performance assessment is to determine the heat exchanger duty, overall heat transfer coefficient, heat exchanger effectiveness, process / utility side pressure drop. Any deviation from the design will indicate occurrence of fouling.
Performance Terms and Definitions
Overall heat transfer coefficient, U
The overall heat transfer coefficient, U, represents how easily the heat can move. A smaller value of U indicates the difficulty in the transfer of heat and vice versa. Heat exchanger performance is normally evaluated by the overall heat transfer coefficient U that is defined by the equation:
When the hot and cold stream flows and inlet temperatures are constant, the heat transfer coefficient may be evaluated using the above formula.
The most commonly used methods for heat transfer analysis are LMTD-F method and the Effectiveness—
NTU method. This section gives an overview of LMTD-F method.
LMTD
The LMTD is Logarithmic Mean Temperature Difference, used to determine the temperature driving force for heat transfer 1n heat exchangers. It is determined by the relationship of the fluid temperature
differences at the terminals of the heat exchanger.
The LMTD Correction Factor, F
If the flow is true counter current, the LMTD calculated is used directly in the basic heat transfer equation. If the flow is not true counter current (1.e., more tube passes than shell passes), LMTD must
be corrected and also to account for cross flow.
In multi-pass shell-and-tube exchangers, the flow pattern is a mixture of co-current and counter current
flow, as the two streams flow through the exchanger in the same direction on some passes and in the opposite direction on others. For this reason, the mean temperature difference is not equal to the logarithmic mean. However, it is convenient to retain the LMTD by introducing a Correction Factor,
F, which is appropriately termed as the LMTD correction factor.
Fouling Factor
One of the important heat-exchanger parameters related to surface conditions is termed as the fouling factor. The fouling factors to be used in the design of heat exchangers are normally specified by the client, based on his experience of running his plant or process to simulate dirt accumulation on the heat transfer surfaces, but if these are not restricted to proper levels, they can totally negate any benefits generated by skillful design. The fouling factor represents the theoretical resistance to heat flow due to a build up of a layer of dirt or other fouling substance on the tube surfaces of the heat exchanger but they are often overstated by the end user in an attempt to minimize the frequency of cleaning. In reality they can, if badly chosen, lead to increased cleaning frequency. The fouling factor increases with increased fouling and causes a drop in the heat exchanger effectiveness. Common types of fouling are chemical, biological, deposition and corrosion fouling.
Industrial Heat Exchangers
The most common types of commercially available heat exchangers are the shell-and-tube exchanger.
Nomenclature
A typical heat exchanger is shown in figure 4.1 with nomenclature.
Heat duty of the exchanger can be calculated either on the hot side fluid or cold side fluid as given
below.
If the operating heat duty is less than design heat duty, it may be due to heat losses, fouling in tubes,
reduced flow rate (hot or cold) etc. Hence, for simple performance monitoring of exchanger, heat duty
may be considered as factor of performance irrespective of other parameter. A deviation in heat duty
may not be a conclusive indicator of fouling due to variation in the process condition. However, the
overall heat transfer coefficient offers itself as a reliable indictor of fouling. Hence the performance
assessment of the heat exchanger is carried out by determination of overall heat transfer coefficient in
the field.
Methodology of Heat Exchanger Performance Assessment
Procedure for determination of Overall heat transfer Coefficient, U
This is a fairly rigorous method of monitoring the heat exchanger performance by calculating the overall heat transfer coefficient periodically. Technical records are to be maintained for all the exchangers, so that problems associated with reduced efficiency and heat transfer can be identified easily. The record should basically contain historical heat transfer coefficient data versus time / date of observation. A plot of heat transfer coefficient versus time permits rational planning of an exchangercleaning program.
The heat transfer coefficient is calculated by the equation
Where Q is the heat duty, A is the heat transfer area of the exchanger and LMTD is temperature driving
force.
The step by step procedure for determination of Overall heat transfer Coefficient is described below.
Step -—A
Monitoring and reading of steady state parameters of the heat exchanger under evaluation are
tabulated as below:
Step —B
With the monitored test data, the physical properties of the stream can be tabulated as required for the evaluation of the thermal data
*MpaS — Mega Pascal Second
Density and viscosity can be determined by analysis of the samples taken from the flow stream at the
recorded temperature in the plant laboratory. Thermal conductivity and specific heat capacity if not
determined from the samples can be collected from handbooks.
Step —C
Calculate the thermal parameters of heat exchanger and compare with the design data

Figure 4.2 Temperature Distributions for a Counter and Co-Current Flow Heat exchanger

7. The LMTD Correction Factor, F
The LMTD correction factor is a function of the temperature effectiveness and the number of tube and
shell passes and is correlated as a function of two dimensionless temperature ratios. Let R and P be
the two dimensionless parameters used to calculate LMTD correction factor defined by the equations
below.
Where,
N = Number of shell-side passes
S, α = Parameters used to calculate LMTD correction factor defined by the equations given above.
8. Corrected LMTD = F x LMTD
9. Overall Heat Transfer Co-efficient
U=Q/(Ax Corrected LMTD)
Heat Exchanger Effectiveness
The heat recovery capability of a heat exchanger is characterized by means of an index referred as the
“Heat Exchanger Effectiveness”, is a measure of thermal performance.
Calculating the heat exchanger effectiveness helps engineers,
¢ To predict how a given heat exchanger will perform a new job.
¢ To predict the stream outlet temperatures without a trial-and-error solution that would otherwise be necessary.
Definition:
“The Heat Exchanger Effectiveness is defined for a given heat exchanger of any flow arrangement as the ratio of the actual amount of heat transferred to the maximum possible amount of heat that could be transferred between the two streams with an infinite area”.
The latter is the rate of heat transfer that would occur in a counter-flow exchanger having infinite heat
transfer area. In such an exchanger, one of the fluid streams will gain or lose heat until its outlet temperature equals the inlet temperature of the other stream.
The fluid that experiences this maximum temperature change is the one having the smaller value of Heat Capacity, C = mass flow rate x specific heat capacity at constant pressure, as can be seen from the energy balance equations for the two streams.
Thus, if the hot fluid has the lower value of C, we will have Tho = Tci and:
Thus, in either case
It should be emphasized that the term effectiveness may not be confused with efficiency. The use of the term efficiency is generally restricted to (1) the efficiency of conversion of energy form A to energy
form B or (2) a comparison of actual system performance to the ideal system performance, under comparable operating conditions, from energy point of view.
Since we deal here with a component heat exchanger and there is no conversion of different forms of
energy in a heat exchanger (although the conversion between heat flow and enthalpy change is present), the term effectiveness is used to designate the efficiency of a heat exchanger. The consequence of the first law of thermodynamics is the energy balance, and hence the definition of the exchanger explicitly uses the first law of thermodynamics.
For air-to-air heat exchangers, when the two streams have the same mass flow (such as the case
of make-up air systems), the expression for the effectiveness referred to as the efficiency) can be
further simplified to:
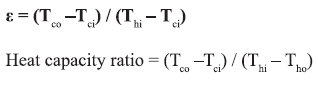
If the effectiveness of a heat exchanger is 0.5, this does not mean that heat exchanger is only 50% efficient in its transfer of thermal energy. By conservation of energy, any energy that is lost on one side must be gained on the other so in that way we would say them as 100% efficient. But the effectiveness is actually just a measure of the ability of a heat exchanger to exchange temperatures.
If a perfect counter flow heat exchanger should be able to get the two fluids to swap temperatures (assuming the same fluid and mass flow rate). If a = 50 °C air and b = 90 °C air going through a perfect heat exchanger, then we should get a = 90 °C air and b = 50 °C air out of it. 50% effective would give 70 °C air out from both streams.
Examples
a) Liquid — Liquid Exchanger
(1) A shell and tube exchanger of following configuration is considered being used for oil cooler with
oil at the shell side and cooling water at the tube side.
Tube Side
1. 460 Nos x 25.4mmOD x 2.11mm thick x 7211mm long
2.Pitch —31.75mm 30° triangular
3.2 Pass
Shell Side
1. 787mm ID
2. Baffle space — 787 mm
3.1 Pass
The monitored parameters are as below:
5. Temperature Range Cold Fluid
7. LMTD Correction Factor, F, to account for Cross flow:
Computing the Parameters below:
8. Corrected LMTD = F x LMTD = 0.977 x 85.9 = 83.9 C.
9. Overall Heat Transfer Co-efficient
Comparison of Calculated data with Design DataHeat Duty: Actual duty differences will be practically negligible as these duty differences could be
because of the specific heat capacity deviation with the temperature. Also, there could be some heat
loss due to radiation from the hot shell side.
Pressure drop: Also, the pressure drop in the shell side of the hot fluid is reported normal (only slightly
less than the design figure). This is attributed with the increased average bulk temperature of the hot
side due to decreased performance of the exchanger.
Temperature range: As seen from the data the deviation in the temperature ranges could be due to the
increased fouling in the tubes (cold stream), since a higher pressure drop is noticed.
Heat Transfer coefficient: The estimated value has decreased due to increased fouling that has resulted in minimized active area of heat transfer.
Physical properties: If available from the data or Lab analysis can be used for verification with the
design data sheet as a cross check towards design considerations.
(ii) In the above example 4.6(a), determine the Effectiveness of heat exchanger and Heat Capacity
ratio.
Hot fluid, Coil = (W x Cph) oil = (719800 x 2.847) / 3600 = 569.24 kW/ °C.
Cold fluid, Cwater = (w x Cpc) water = (881150 x 4.187) / 3600 = 1024.83 kW/°C.
Therefore,
Cmin = 569.24
Cmax = 1024.83
Q = 24477.4kW
ΔTmax = 145- 25.5 = 119.5°C
b) A Plate Heat Exchanger with total heat transfer area of 41 m2 is used to exchange heat between a
hot effluent stream and cooling water stream.
The monitored parameters are given below:
Calculate LMTD and Overall heat transfer coefficient, U, assuming LMTD correction factor of 0.9
for plate heat exchanger. Specific heat capacity of hot effluent stream is 4.187 kJ/kg°C.
Solution
Hot Load, Q = (85200 x 4.187 x (77-54)) / 3600 = 2279 kW.
LMTD, Counter flow = {(77-57) — (54-49)}/ {In (77-57) / (54-49)}
= 10.8°C
Correction Factor, F = 0.9 (given)
Corrected LMTD =FxLMTD
=0.9 x 10.8 =9.72°C
Overall heat transfer coefficient, U = Q / (A x Corrected LMTD)
U = 2279 / (41 x 9.72) = 5.718 kW/m2. °C
c) A double pipe heat exchanger is used to cool a hot stream from 177° C to 121° C by heating a cold
stream from 49° C to 77° C. The hot stream will flow in the inner pipe in a counter flow arrangement
to the cold stream in the outer pipe.
The heat transfer surface area of 18.5 m? will transfer the heat load of 1025.85 kW. Determine the
overall heat transfer coefficient, U.
Solution
LMTD, Counter flow = {(177-77) — (121-49)}/ {In (177-77) / (121-49)}
= 85.2°C
Overall heat transfer coefficient, U =Q/(Ax LMTD)
= 1025.85 / (18.5 x 85.2)
= 0.651 kW/m2 °C
d) Surface Condenser
A shell and tube exchanger of following configuration is considered being used for Condensing turbine
exhaust steam with cooling water at the tube side.
Tube Side
20648 Nos x 25.4mmOD x 1.22mm thk x 18300mm long
Pitch — 31.75mm 60° triangular
1 Pass
The monitored parameters are as below:
Heat Duty: Actual duty differences will be practically negligible as these duty differences could be
because of the specific heat capacity deviation with the temperature. Also, there could be some heat
loss due to radiation from the hot shell side.
Pressure drop: The condensing side operating pressure raised due to the backpressure caused by the
non-condensable. This has resulted in increased pressure drop across the steam side.
Temperature range: With reference to cooling waterside there is no difference in the range however,
the terminal temperature differences has increased indicating lack of proper heat transfer.
Heat Transfer coefficient: Heat transfer coefficient has decreased due to increased amount of noncondensable with the steam.
Trouble shooting:
Operations may be checked for tightness of the circuit and ensure proper venting of the system. The
vacuum source might be verified for proper functioning.
Solved Example:
4. Energy Performance Assessment of Heat Exchangers
Flow rates of the hot and the cold water streams flowing through a heat exchanger are 12 and 30 kg/
min, respectively. Hot and cold water stream inlet temperatures are 72 °C and 27 °C, respectively. The
exit temperature of the hot stream is required to be 52 °C. The specific heat of water is 4.179 kJ/kg K.
The overall heat transfer coefficient is 800 W/m2 K.
Neglecting the effect of fouling, calculate the heat transfer area for
a) Parallel-flow
b) Counter-flow
Solution:
















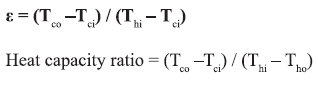











Comments
Post a Comment